Some of the most interesting features of this mystery called Bigfoot revolve around the reputed size, agility and strength of these rather ubiquitous creatures. Much has been written on these subjects by a wide variety of investigators and the famous Patterson film confirms (to believers, including this author) the distinctly large size of at least one specimen. Also, circumstantial (i.e., sighting) evidence abounds as to the supposed running speed and agility of these bipeds. This paper will attempt to produce estimates of Bigfoot weight, circumferences, speed, strength and agility based upon simple mathematical and biomechanical concepts (with procedures not previously documented by other investigators). Of course, some "reasonable" assumptions have to be made throughout this discussion; but after all, we don't have one of these remarkable mammals to test. Finally, this essay will take a look at the probability of the existence of such unparalleled creatures based upon an uncomplicated, statistical methodology.
Weight Estimates
Weight estimates by
witnesses vary considerably. It is certainly not an easy task to estimate
something that is well outside of the normal human weight range. The difficulty
is surely compounded by the stunning and/or frightening realization of
what the witness is viewing. Even the estimates made of Patty's weight
have ranged from the sublime (300 lbs.) to the ridiculous (2,000 lbs.).
However, a method will be described that produces quite acceptable estimates
by scaling a baseline value to whatever height desired.The baseline utilized
by this author is that of a 6' tall mountain gorilla, with adjustments
made due to the gorilla's very short legs and long torso. The recorded
450 lb. weight of captive gorillas would be reduced quite considerably
if the leg and torso lengths were proportioned as with a human (or Bigfoot).
Otherwise, the short neck, barrel chest and long thick arms of a gorilla
correspond very closely with many eyewitness descriptions of a Bigfoot.
Thus, for the purpose of establishing a baseline, this author is presuming
the weight of a 6' tall Bigfoot at 300 lbs. Note that this value is on
the very high side of human ranges, yet certainly reasonable considering
the reputed thick structure, high shoulders and long arms of a Sasquatch.
At this point, it is possible to scale weight to any height, assuming the relative structural build stays constant. The relation that is used to define weight, W, versus height, H, is,
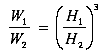 (1)
(1)
To maintain the constant build requirement, any percentage increase in height is accompanied by the same percentage increase in all circumferential measurements. However, since the cross-section area of any body segment increases with the square of the circumference (or radial dimensions, R), the equation above was basically derived from the relationship,
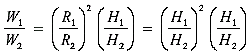 (2)
(2)
This relation is valid for practically any cross-section shape, i.e., rectangular, elliptical, circular, etc. It is now possible to tabulate estimates of Bigfoot weight using the presumed 6' tall/300 lb. baseline. Table 1 below uses Equation (1) to give those estimates, along with two other related columns. For referral purposes, the first column uses a baseline of 6' and 200 lbs. for a fairly "robust" human male and employs the same equation from above to predict human weights versus height.
The third column of Table 1 uses another baseline reference. One of the more interesting stories of Bigfoot lore concerns the supposed (but very well documented) capture of a young Bigfoot by a train crew in B.C over 115 years ago. This creature, named Jacko by the locals, was reported to be 4' 7" tall and 127 lbs. These measurements are set as the baseline for the last column's tabulations and can be compared with the results of the second column. Note that the baseline measurements used for scaling in each column are emphasized in the table. The 7' 3" height is included in the computations since that is the most recent estimate of height for Patty.
| Table
1 Extrapolated Weight Estimates |
|||
| Male Human |
Adult Bigfoot |
Jacko |
|
| 5' 6" | 154 lbs. | -- | 219 lbs. |
| 6' 0" | 200 lbs. | 300 lbs. | 285 lbs. |
| 6' 6" | 254 lbs. | 381 lbs. | 362 lbs. |
| 7' 0" | 317 lbs. | 476 lbs. | 452 lbs. |
| 7' 3" (Patty?) | 352 lbs. | 529 lbs. | 502 lbs. |
| 7' 6" | -- | 586 lbs. | 556 lbs. |
| 8' 0" | -- | 711 lbs. | 675 lbs. |
| 9' 0" | -- | 1012 lbs. | 961 lbs. |
Circumferential Estimates
A similar, but slightly more complicated scaling method is presented to predict realistic (?) circumferential measurements of a Bigfoot. In this instance, the dimensions of a presumed 8' tall, 711 lb. Sasquatch (from Table 1) will be estimated. This process requires two steps
- The known dimensions of a 6' tall, 234 lb. heavyweight boxer will be scaled to a 6' tall 300 lb. weight.
- Those dimensions will then be scaled to 7' and 8' heights, with the corresponding weights given from Table 1.
Note that the basic build of this, mesomorphic (and decidedly stout) boxer is somewhat different from the presumably, more thickly, proportioned Sasquatch. However, it is as good of a starting point as any. Table 2 below summarizes the results of this process. Eq. (2) was utilized to compute the R ratios (or circumferential ratios), with height and weight values being presumed from the previous arguments. It is also assumed through all of this discussion that the body density of a Bigfoot is very similar to that of a human. The anecdotal reports of their swimming ability would imply as much.
| Table
2 Circumferential Estimates |
||||
| 6' / 234 lb. Heavyweight | 6' Scaled to 300 lbs. | 7' / 476 lb. Bigfoot | 8' / 711 lb. Bigfoot | |
| Neck | 20" | 22.5" | 26" | 30" |
| Chest | 42.5" | 48" | 56" | 64" |
| Biceps | 17" | 19" | 22" | 25" |
| Forearm | 14" | 16" | 18.5" | 21.5" |
| Waist | 34" | 38.5" | 45" | 51.5" |
| Thigh | 26.5" | 30" | 35" | 40" |
| Calf | 17" | 19" | 22" | 25" |
The essence of the calculations contained in the last column of Table 2 is that these dimensions are believed to be sufficient for an 8' tall Bigfoot to weigh 711 lbs. Basically, these dimensions would create a satisfactory volume for that weight. In the unlikely event that the body density of an adult Bigfoot is greater than that of the aforementioned muscular, human model, then the listed circumferences could be reduced slightly. Also, if these tall creatures have distinctly non-human length of arms or torso, the dimensions listed above could again be reduced somewhat.
Needless to say, a limited amount of correlating data from eyewitnesses is available. However, the famous encounter narrated by Albert Ostman did include some size estimates for the old female and the two males. He noted that the massive 8' male would require over a 30" collar and that the 7'+ female would weigh over 500 lbs., which compares well with Patty's estimate from Table 1. Also, he estimated that the adolescent 7' male would weigh about 300 lbs., with a 50-55" chest and a relatively trim 36-38" waist. The figures from Table 2 suggest a much more stoutly proportioned 7' adult, especially in the waist. A sharp reduction in the waist dimensions and some reduction in the chest and legs would be required to reduce the 476 lb. tabulated weight to the 300 lbs. assessed by Ostman. Of course, there is no reason to believe all Sasquatch fit the massive model described above. At a minimum, the adolescents need time to "fill out", just as our human species requires.
Speed Estimation
Numerous observers have made speed estimations of a Bigfoot in sprinting mode (or at some unknown portion of full stride). Some of the purported observations have been made by witnesses pacing a large bipedal creature with their automobile. Almost without variation, observers describe either the walking or running stride as quite fluid, or graceful, in its essence.
This report will attempt to make speed estimates based upon the simple scaling of human sprinting mechanics. Some minimal hypotheses are submitted in this discussion.
- The bipedal gait, i.e., kinematics, of a running Sasquatch does not markedly differ from the bipedal gait of a human. The mechanics of running are quite complex, but there is no reason to believe there are any great differences between our species and Bigfoot.
- The foot structure of a Sasquatch is as described by the theoretical analysis of the late Dr. Krantz. In other words, the foot structure of these large bipeds may be contributory to the long, flat-footed running style so often described by witnesses as "fluid". Note that the forward positioning of the ankle, and the attendant distal connectivity of the tendons as theorized by Krantz, would provide mechanical leverages well suited for climbing but would not be the ideal model for a hominoid sprinter.
The human model to be used (i.e., directly scaled) for this estimate is a quite "average" sprinter with a proportionately long, fluid stride, namely this author as a high school runner many years past. The stride of this 5'7" runner was 7.5' and at maximum speed, 4.2 strides per second were taken. This works out to a top speed of 21 mph. (For comparison, a typical world-class sprinter takes an approximate 8' stride at 4.9 strides per second, for a maximum of 27 mph). Also, as an extreme example, this author recalls a 6' 2" Olympic sprinter in the early 60's with a reputed 9' 3" stride.
The direct scaling of stride length versus height (5' 7" versus 8') would predict a 10.74' stride for an 8' Sasquatch. At the same 4.2 strides per second, the top speed would compute to a maximum 31 mph sprint. If one uses the world-class human comparison at 4.9 strides per second, the top speed of our prototype Sasquatch works out to 36 mph. In either eventuality, these calculations would seem to discount some of the more extreme estimates of speed (> 45 mph) that have been ascribed to a Bigfoot by a few observers. However, the concept of "quickness", "agility" or the remarkable acceleration commonly attributed to these creatures is another matter entirely, and will be broached after the next section.
Strength Estimate
A methodology that utilizes the speed estimates from above, a smattering of rigid body mechanics, and derivations from calculus will be employed to make a strength evaluation of our representative 8' Sasquatch. Fortunately, the readers of this essay will not be required to perform the mathematics behind this analysis. Only the simplest, technical highlights will be presented, along with the appropriate explanations.
The kinematics of bipedal running are certainly quite complex, but it should not be a mistaken conjecture to assign great similarities with the gait and physical mechanics of a Sasquatch to a human counterpart. Numerous observers have almost universally implied that the movements are very human-like. Without making this discussion more complicated than it need be, the motion of a leg in full stride requires that certain hip muscles contract at the top of each stride, provide a twisting (i.e., torque) load to the leg mass pivoting below. Note that the leg is momentarily at rest at the beginning of each stride. At that time these muscles produce a maximum angular acceleration of the leg mass. The physics of this action can be ascertained as the applied torque equaling the mass moment of inertia of the leg times the angular acceleration of the leg, or
![]()
Referring to the previous section, the angular acceleration of the prototype Bigfoot leg should be nearly identical to that of the human counterpart. This is certainly true if the number of strides per second are equivalent, as has been postulated previously. However, the great difference between the representative human and the Sasquatch is in the value of the mass moment of inertia of the leg structure. Without going into the mathematical niceties of the calculation, the definition of mass moment of inertia for a "rod", pivoting about one end, with mass, m, length, L, and maximum elliptical cross-section radius, a, is given as,
![]()
It is important to realize that the next calculation of applied torque (i.e., strength) for the human and the Sasquatch is not dependent upon the assumed cross-section shape of the leg mass. (The result is the same whether Eq. (3) is derived for an ellipse, circle, rectangle or any other general shape of the leg sections). Now the comparison of strength for Sasquatch versus human can be evaluated. Eq. (3) above can be stated as a ratio,
![]() (3)
(3)
or,
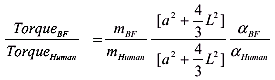 (4)
(4)
giving
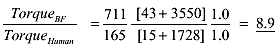 (5)
(5)
The only mathematical assumptions here are as follows:
- The leg mass ratio is the same as the body mass ratio (711/165).
- The leg length ratio is the same as the height ratio (96/67).
- The cross-section radius ratio is proportional to leg circumference ratio (40/24).
- The 4.2 strides per second, presumed for both the 8' Bigfoot and the human representation, would strongly suggest the same maximum angular acceleration, a, for both.
- General physical strength of the Sasquatch is no different than that derived for the specific body part evaluated here, namely, the applied couple (torque) produced by the hip muscles.
Note that if the Sasquatch can sprint at 4.9 strides per second, the calculation in Eq. (5) will indicate an applied torque/strength ratio of 10.4. These values can be viewed in light of reputed strength of other primates. Chimpanzees (with near human weight) have been estimated to possess five times human strength and gorillas supposedly have 10 times human strength. The hypothetical strength levels computed above at least pass the "common sense" test for such a large hominid. No assessment is set forth for the (obviously) unknown distal connectivity (i.e., mechanical leverage) of a Bigfoot's muscle-to-bone structure. It is this author's opinion that the coarse estimates displayed above are, essentially, conservatively low. Lifestyle issues of these large mammals would certainly dictate an exceptionally well-conditioned body. Finally, to put this strength assessment into perspective, it is not inconceivable that these reclusive hominids can bench-press a ton and leg press the car in your garage.
The Agility Implication
Perhaps even more significant than the strength levels presented above are the associated "agility" (or "quickness", or "acceleration") factors that are implicit in the preceding calculations. The ability to accelerate is directly proportional to the ratio of applied force to the mass being moved, as Sir Isaac Newton so wisely observed. The concept of acceleration is often expressed, by those not concerned with the mathematics of physics, as the general observation of quickness or agility. Using our same human comparison and the preceding computations, one can define the strength-to-weight ratio of the Sasquatch versus the human counterpart with the rather simple relation,
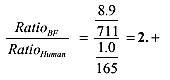
Based upon this uncomplicated calculation the implications of Bigfoot agility, in comparison to the human example, are quite significant. First, it would indicate that these creatures would be able to attain their top running speed in half the time of our human comparable. Since a human sprinter requires 5 to 6 seconds to obtain maximum speed, the Sasquatch would only need 3 seconds. This physical attribute would certainly come in handy while hunting (i.e., ambushing) elk or deer, assuming, of course, that this activity is part of their lifestyle. In a similar vein, the ability to make sudden movements would be advantageous in snatching "quicker" food sources, such as fish or small mammals.
Secondly, this strength-to-weight ratio would imply an exceptional ability to climb. Imagine how easy it would be to move up a hill if one's human body mass were effectively reduced in half, yet all previous strength was maintained. Additionally, if the foot structure of a Sasquatch is as hypothesized by Dr. Krantz, the mechanical leverages would further enhance their climbing abilities. There are certainly very many witnesses who have reported the extraordinary quickness that these creatures have displayed bounding up steep embankments when surprised by the human encounter. Note, of course, that none of this discussion is offered as proof in any form; it is left to the reader to draw all inferences and conclusions. The last section of this essay will expound upon this concept, namely, can it all be true?
. . . Fools and Liars, All?
Perhaps the most difficult aspect in accepting the existence of such shadowy creatures in our very own back yard is that, essentially, the concept defies common wisdom (and academic approval). This is especially true for those with only casual knowledge of this mystery's scope.
It is useful to reiterate several observations provided by other investigators.
- First, the concept of maintaining an ironclad hoax for well over a century is beyond the pale. The wide spectrum of observers and the time/geography involved serve, realistically, to make it an unrealizable task in carrying out such a hoax.
- Also, detailed analysis of certain aspects of the reported evidence is remarkably consistent. For example, the mathematical analysis of recorded footprint lengths (as set forth by other investigators) describes an excellent fit to the well-known Gaussian distribution (i.e., "Bell curve"). The difficulty in faking such a distribution over a large time frame and wide geographical span is practically insurmountable. Equally significant, documented compilations of eyewitness' estimates of height indicate a trend that slowly increases with northern latitude of the observation. Considering that a mammal's ability to maintain body temperature in cool climates is benefited by increased body size, the trend described is, at least, notable and reasonable.
As a final evaluation, a simple probabilistic approach will be employed to assess the credence of the large number of eyewitness reports. The method employed herein will be to evaluate the so-called "null hypothesis", which is merely a technique to affirm a viewpoint by effectively disproving the opposing position.
For example, let us conservatively state that the probability of any particular eyewitness report being either a deliberate hoax or the product of incompetent observation as being 99%! Then, let us take the 100 "most believable" reports and determine the probability that all of these reports are false. Based upon simple theory of compound probability, the chance that all are false can be shown to be,
.99100 = .366 = 36.6%
The null hypothesis would then dictate that the probability is 1.0 - .366 = 63.4% that at least one report was produced by an honest, competent observer. Since the number of recorded observations is far greater than 100 and it is similarly doubtful that 99% of the general public are worthless interpreters, the actual probability that at least one report is valid is well over 99%.
In conclusion, there
is certainly no proof of the existence of such reclusive hominids contained
within this dissertation. But the one thread of "truth" that this author
wishes to convey is that the hypothetical analysis presented herein is
independently generated, yet quite consistent with many eyewitness accounts.
Perhaps the only aspect of this mystery that is more preposterous than
its circumstantial/factual substance is the chance that it is all a superbly
conducted ruse.
Back to Biology, Scientific Papers and Field Reports
Back to What's New?
Back to Newspaper & Magazine Articles
Home/Main
Portions of this website are reprinted and sometimes edited to fit the standards of this website under the Fair Use Doctrine of International Copyright Law
as educational material without benefit of financial gain.
http://www4.law.cornell.edu/uscode/17/107.html
This proviso is applicable throughout the entire Bigfoot Encounters Website.